Series Matematika kali ini kita akan mengulas kembali (bagi yang sudah pernah belajar) atau belajar Trigonometri (bagi yang belum belajar).
Pada materi sebelumnya kita sudah membahas tentang Segitiga, sekarang kita masih akan membahas seputar segitiga juga mulai dari menghitung Luas, sudut dan panjang sisi-sisi nya.
Seperti kata dasar nya, Trogonometri berasal dari bahasa Yunani "Trigonon" = Segitiga dan "metron" = mengukur namun mengukurnya kali ini akan menggunakan Bantuan Sinus,Cosinus Dan Tangen.
Segitiga Siku-Siku
Dalam segitiga siku-siku, setiap sisi dari Segitiga diberi nama sesuai dengan posisinya terhadap sudut yang di observasi. Ada 3 nama yang diberikat yaitu
1. Ajasen (Adjacent ) : sisi yang bertetangga dengan sudut observasi
2. Oposit ( Opposite ) : sisi yang bersebrangan dengan sudut observasi
3. Hipotenusa ( Hypotenuse) : Sisi terpanjang atau sisi yang bersebrangan dengan sudut Siku-siku
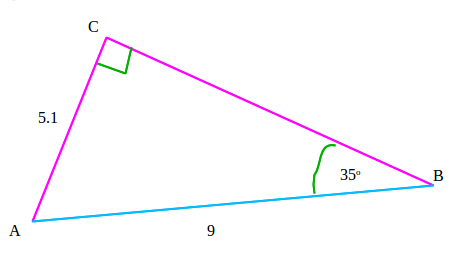
Mari kita namai masing-masing sisi dari segitiga diatas. Dengan sudut observasi alpha di A maka sisi :
AC = Ajasen ( Adjacent ) karena sisi AC bertetangga langsung dengan sudut alpha
BC = Oposit (Opposite ) karena sisi BC bersebrangan dengan sudut alhpa
AB = Hipotenusa karena sisi AB merupakan sisi terpanjang atau bersebrangan dengan sudut siku-siku
Sekarang coba tentukan nama masing-masing sisi segitiga berikut
Rumus-rumus Trigonometri Segitiga Siku-siku ( Right Triangle )
Perhatikan Segitiga disamping
Sin (a) = Opposite / Hipotenusa
Cos (a) = Adjacent / Hipotenusa
Tan (a) = Opposite / Adjacent
Dengan rumus-rumus diatas kita bisa mencari panjang sisi-sisi,besar sudut nya maunpun nilai dari Sin,Cos dan Tan
Contoh :
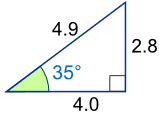 JIka diketahui sisi-sisinya dengan sudut 35' , tanpa kalkulator, berapa nilai sin (35) ?
JIka diketahui sisi-sisinya dengan sudut 35' , tanpa kalkulator, berapa nilai sin (35) ?
Jawab :
Sin (a) = Opposite / Hipotenusa
Sin (35) = 2.8 / 4.9 = 0.57
Contoh lain
Dari segitiga diatas coba cari panjang sisi BC. setelah mengetahui rumus-rumus Trigonometri untuk segitiga siku-siku kita harus menentukan apakah harus diselesaikan dengan Sin, Cos atau Tan. Dari informasi segitiga diatas maka yang pas adalah dengan menggunakan Tan , dengan rumus Tan(a) = Opposite / Adjacent . karena dengan sudut di B yang besar nya sudah ada dan diketahui pula adjacent nya yaitu sisi AC = 5.2
Jadi :
tan (35) = 5.1 / BC
0.7 = 5.1 / BC
BC = 5.1 / 0.7 = 7.3
*Gunakan kalkulator untuk mencari tan(35)
Selain dengan Tan, bisa juga dengan Cos (a) = Adjacent / Hipotenusa
cos(35)= BC / 9
0.82 = BC / 9
BC = 9 x 0.82
= 7.3
masih dari segitiga diatas, Jika sisi AC tidak diketahui, maka bisa dicari dengan rumus sin(a) = Opposite / Hipotenusa
sehingga sin(35) = AC / 9
0.57 = AC / 9
AC = 9 x 0.57
AC = 5.1
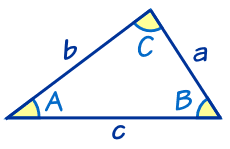
Rumus trigonometri Segitiga selain Siku-siku
Untuk segitiga selain siku-siku berlaku rumus-rumus berikut
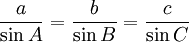 ( Hukum sinus)
( Hukum sinus)
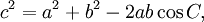 ( Hukum Cosinus)
( Hukum Cosinus)
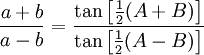 ( Hukum Tangen)
( Hukum Tangen)
Dengan rumus diatas , sudah mudah bukan menyelesaikan soal-soal seputar segitiga ? . Silahkan latihan sendiri selanjutnya :D
Identitas Trigonometri
Dari formula ini
sin(a) = Opposite / Hypotenuse
cos(a) = Adjacent / Hypotenuse
tan(a) = Opposite / Adjacent
Dapat kita otak-atik, substitusi satu sama lain seperti berikut:
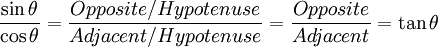
Artinya : tan(a) = sin(a) / cos(a)
misal tan(35) = sin(35) / cos(35)
= 0.57 / 0.82
= 0.7 , buktikan dgn kalkulator tan (35) , maka nilainya akan sama yaitu 0.7
masih ada Identitas trigonometri yang lain, silahkan cari :D
Baca juga
6 Trik Mudah Matematika
ref : math is fun